Problem Description: The real-time system consists m resources and
n periodic tasks, G
= {T1, …, Tn },
in which each task Ti = (ci,
pi) is characterized
by its execution requirement ci
and its period pi. The deadline for each task
instance is the task's next period. ci
and pi are integer
multiples of a system unit time. The weight (or utilization) for
task Ti is defined as wi
= ci/pi, and
the system utilization is the summation of all tasks' utilizations
U =
Swi
(U
£
m). The problem is to
design a scheduling algorithm with the following constraints: (C1).
A resource can only be allocated to one task at any time,
that is, resources can not be shared concurrently; (C2) A task can
only be allocated at most one resource at any time, that is, tasks
are not parallel and thus cannot occupy more than one resource at
any time.
Current Solutions: An optimal scheduling algorithm (Pfair)
[1] has been proposed. But, the Pfair
algorithm incurs a very high scheduling overhead by making
scheduling decision for every time unit to enforce
strict proportional progress for each task at any time unit,
which prevents it from being employed in practice, as many of its
variants. To reduce the scheduling overhead, notice that deadline
misses happen only at the end of tasks’ periods, we
proposed a novel idea of boundary-fair (Bfair)
scheduling [2], which makes scheduling decision at a period boundary
to ensure that all tasks with deadline as next period boundary will
finish on time, and to properly allocate resources to
the rest tasks such that they can meet their deadlines in the
future. A schedule Bfair
iff any task Ti
is either allocated ëwi*tbû
or éwi*tbù
units at any period boundary time tb.
Bfair algorithm is also
optimal in the sense that it can achieve full system utilization.
And by making scheduling decisions at periodic boundaries, it
effectively reduces the number of scheduling points as well as
context switches. We showed that Bfair
algorithm has the same complexity as that of
Pfair algorithm for each scheduling point, but with fewer
scheduling points. Thus, it will reduce the overall scheduling
overhead compared to Pfair algorithm,
which is especially important when they are used on-line. We believe
it will attract researchers' attention from
Pfair to boundary-fairness.
Consider an example task set that has 6 tasks
T1=(2, 5),
T2=(3, 15),
T3=(3, 15),
T4=(2, 6),
T5=(20, 30),
T6=(6, 30).
Here, LCM = 30, Swi
= 2. The proportional-fair schedule generated by
Pfair scheduling
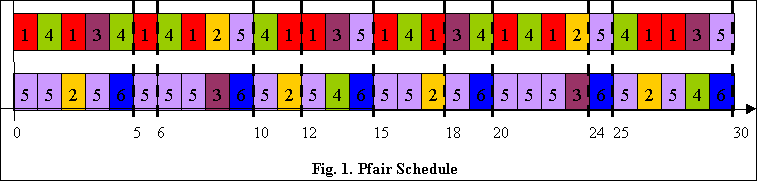
algorithm in [1] is shown in Fig. 1 (the dotted bold lines are
period boundaries) with 30 scheduling points and
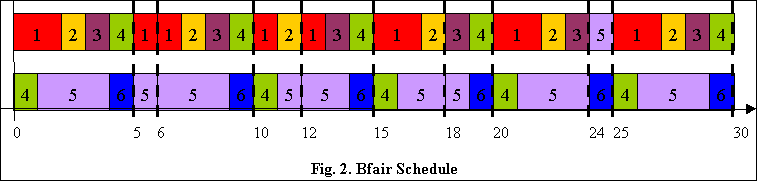
60 context switches. The boundary-fair schedule generated
by Bfair scheduling algorithm in [2] is shown
in Fig. 2 with only 11 scheduling points and 46
context switches.
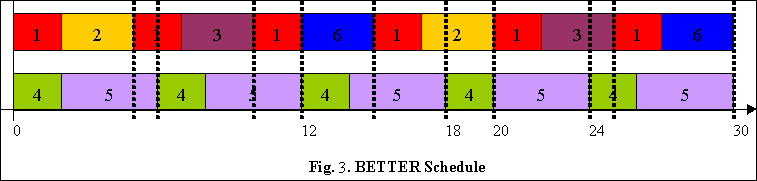
Can we do better than the schedule above? Yes.
If tasks are in the order of T1, T2, T3,
T6, T4, T5,
the first four tasks could be scheduled on one resource while the
last two task were scheduled on another resource. We can get the
BETTER scheduling as shown in Fig. 3 where there are only
29 context switches (considering scheduling points
effect). However the ordering of tasks is NP-hard.
Future work: Exploring ideas to further
reduce the scheduling overhead and incorporating other issues in
parallel scheduling (such as synchronization and migration) would be
the next step in this direction. Also, a real implementation of the
algorithm and the performance comparison with previous efficient Pfair variants will also be pursued. A comprehensive list of
publication on the fairness scheduling algorithms can be found from
the website of
Prof. James H. Anderson (University of North Carolina at Chapel Hill).
[1]
S. K.
Baruah, N. K. Cohen, C. G. Plaxton,
and D. A. Varel. Proportionate
progress: A notion of fairness in resource allocation.
Algorithmica, 15(6):600–625, 1996
[2]
D. Zhu, D. Mosse and R.
Melhem, Periodic Scheduling Problem
for Multi-Processor Real-Time Systems: how much fairness is
necessary? IEEE Real-Time System Symposium 2003