


Next: Recursive Formula and Time
Up: STRATEGY DYNAMIC PROGRAMMING
Previous: Divide and Conquer Solution
- A1 X A2 = (A1) X (A2)
- Partition at k=1: Subproblems (A1) and (A2)
- cost of (A1) is M[1,1] and that of (A2) is M[2,2]
- cost of combining (A1) and (A2) into one is
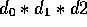 .
. -
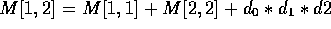 .
. - M[1,2] = 0+ 0 + 1200 = 1200.
- A2 X A3 X A4 = (A2) X (A3 X A4) (k=2)
Or, = (A2 X A3) X A4 (k=3).
- k=2: cost= M[2,2] + M[3,4] + d1*d2*d4
- k=3: cost= M[2,3] + M[4,4] + d1*d3*d4
-
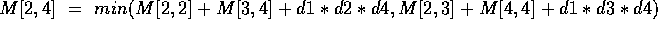
In short,
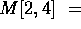
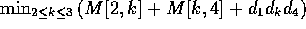
- A2 X A3 X A4 X A5
= (A2) X (A3 X A4 X A5) (k=2)
Or, = (A2 X A3) X (A4 X A5) (k=3)
Or, = (A2 X A3 X A4) X (A5) (k=4)
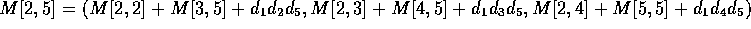
- In general, by factoring
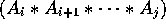 at kth index position
into
at kth index position
into
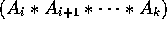 and
and 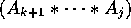 need M[i,k] + M[k+1,j] multiplications and
creates matrices of dimensions
need M[i,k] + M[k+1,j] multiplications and
creates matrices of dimensions 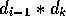 and
and 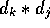 . These
two matrices need additional
. These
two matrices need additional 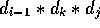 multiplications to combine.
multiplications to combine.
Sushil Prasad
Thu May 13 13:06:05 EDT 1999
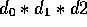 .
.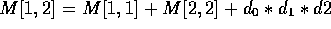 .
.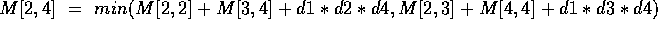
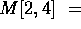
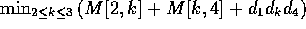
![]()