Graph Coloring

1. Guess a coloring

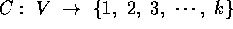
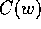is the color of node w

2. Verify that the guess is correct
for all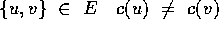

Step 1
Step 2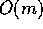
Total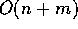

What if one allows ability to guess correctly, if there exists a correct guess?

Non Deterministic Algorithm will be polynomial time if verification is polynomial.

Definitions

Problem : Coloring

Instance I: a graph G and number of colors k

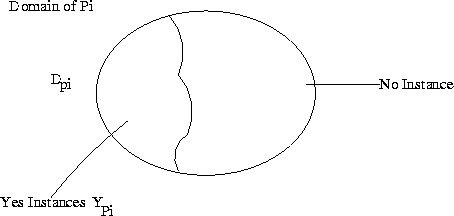
No Instances

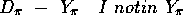
Polynomially Bounded Non-Deterministic algorithm is whose 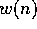is polynomial for all yes instances.

NP: a class of decision problems which have polynomially bounded non-deterministic algorithms.

NP contains those problems whose guesses are polynomial time verifiable.

Coloring NP

Clique NP

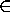SAT NP
guess: a truth assignment
T: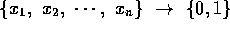

check: verify that each clause is satisfied
for all c 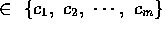c has at-least one true literal.

time analysis
guess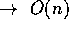
check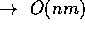
total 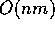is bounded by a polynomial in length of input O(nm)

Clique NP

Sorting NP, but no guess needed