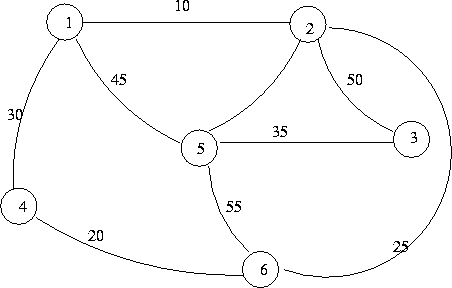
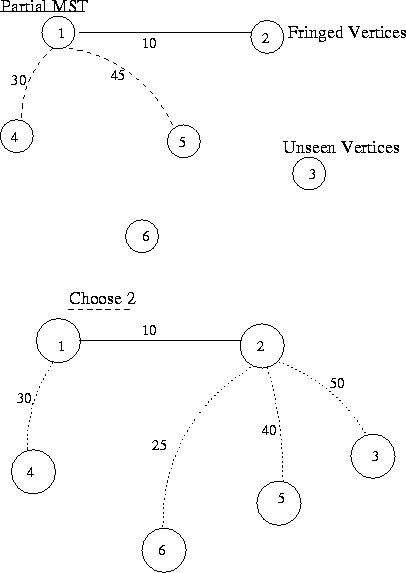
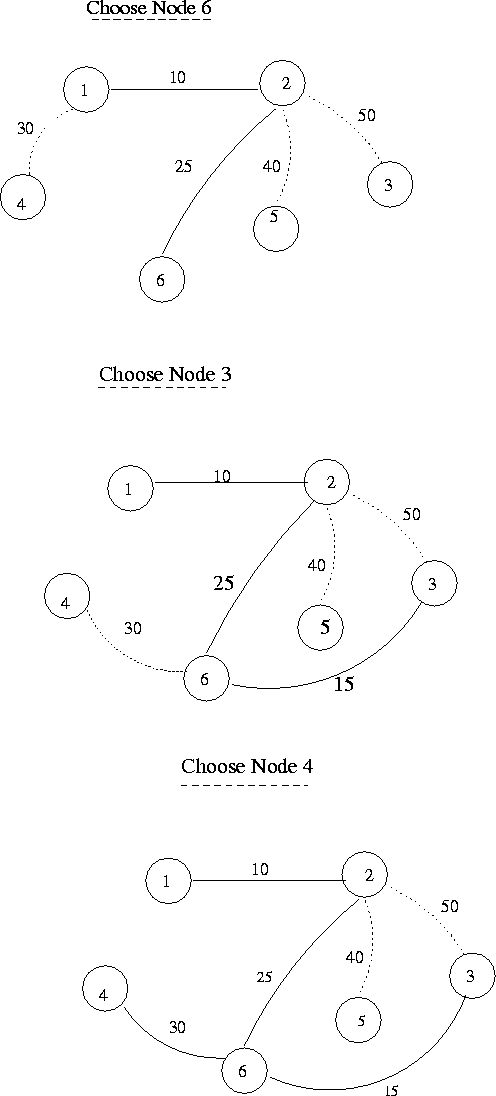
PRIM-DIJKSTRA'S MST ALGORITHM

PRIM-DIJKSTRA'S MST ALGORITHM

Input: G=(V,E,W)
Output:

Select a vertex and move v to

For i=1 to n-1 do

Let be an edge such that , and for all such edges, has the minimum weight.

endfor

Theorem: Let be a weighted connected graph and be a MST of G. Let is a subtree of T. If is the minimum weight edge such that and then is a subtree of a MST of G.

Proof:

1. If , done
2. Let
   Then has a cycle:

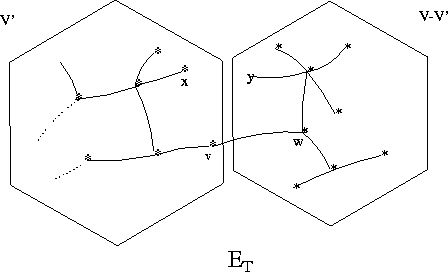
By the choice of

Consider
Its weight is no more than the weight of T and it is a spanning tree.
is a subtree of a MST of G

• Data Structure for Prim's Algorithm
• Modified Prim's Algorithm