Let T be the spanning tree for G generated by Kruskal's algorithm. Let
be a minimum cost spanning tree for G. Show that both T and
have the same cost.
Proof:If edges of T and are the same, we are done.
Let 
.
Let e be a minimum cost edge such that 
and
i.e e is minimum cost edge in 
Inclusion of e in creates a cycle. Let 
be this cycle.
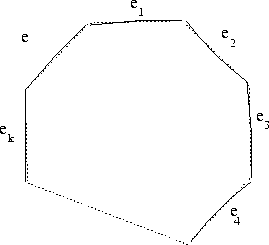
At least one of 
through 
is not in T else e will form cycle
in T as well.
Let that edge be 
.
If 
then 
would be selected by Kruskal's algorithm
first and included into T. But .
(because of choice of e, would have been considered for inclusion in a subset 
of 
. Hence, would not form a cycle in because 
.)
Consider 
Here the cycle created by 
is broken by
Cost of 
is no more than that of which does not have e
in it.
Repeat this process for all such edges in 
to
eventually convert into T without increasing cost.
Hence, T is a minimum spanning tree.
(Thus, greedy strategy which is locally optimal decision leads to a global optimal solution for spanning tree problem.)