


Next: Sample Test 2
Up: root
Previous: Some Reference Books for
NAME: Questions to be graded:--------
Design and Analysis of Algorithms
Test 1
Summer 2009
Notes
- Answer any four. You have 75 minutes.
- Show your work, as partial credit will be given.
Write neatly and to the point.
State algorithms at an abstract level.
- Use both sides of the answer sheet, start each answer on a new page,
and arrange your answers in increasing order of their question numbers. Write
your name and the four question numbers
that you want graded at top right of the first page. If you do not,
then your first four answers will be graded in case you have attempted more.
Questions
- (15 points)
Prove that
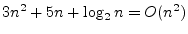 by definition 2 and
by definition 3.
by definition 2 and
by definition 3.
OR
A 3-way search (instead of a binary search)
compares the key with the values at locations 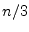 and
and 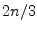 of a
of a
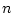 -size array, and then recursively searches in one of the three intervals.
Set up a recurrence relation for the worst-case time complexity of
3-way search, and solve it.
-size array, and then recursively searches in one of the three intervals.
Set up a recurrence relation for the worst-case time complexity of
3-way search, and solve it.
- (15 points) State the tree (insertion) sort, odd-even
transposition sort, and quicksort
algorithms in 3-4 sentences each, and estimate, with suitable but brief
justification,
their (i) average case
time complexities and (iii) their worstcase space complexities.
Use known properties of binary search trees in case of tree sort
and intuitive arguments about the other two to justify average
case scenarios.
- (15 points) State a situation with suitable but brief justification, if any, when you would prefer
(i) linear insertion sort over binary insertion sort,
(ii) heapsort over quicksort,
(iii) quicksort over mergesort,
(iv) tournament sort over sorting by ranking,
and (v) odd-even exchange sort over bubble sort.
- (15 points) Distinguish between time complexity and problem complexity.
Briefly state the milestones (in terms of time complexity)
we arrived at in the process of developing binary search
algorithm starting from the sequential search and proceeding via jump
search. Why did we not look further than the binary search algorithm?
What was the role of decision trees in this process?
- Set up a recurrence relation for the depth of the stack for quicksort
assuming that the sizes of the left and the right partitions are compared
and quicksort is recursively called on the smaller partition only.
There is no recursive call on the larger partition because of
tail recursion. By solving
this recurrence relation, show that the depth of the stack is bounded by
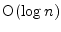 on a list of
on a list of 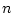 integers.
integers.
- (15 + bonus 5 points) Prove that a lower bound on problem complexity of
comparison-based sorting algorithms is
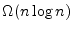 .
.



Next: Sample Test 2
Up: root
Previous: Some Reference Books for
Sushil_Prasad
2014-08-26