


Next: Student Information
Up: root
Previous: Sample Test 2
NAME:
Questions to be graded:
CSC 4520/6520: Design and Analysis of Algorithms
Test 3
Summer 2009
Notes
- Answer any six problems. Start each answer in a different page. Time =100 minutes.
- Do not spend too much time on any problem. Read them all through
first and attack them in the order that allows you to make the most progress.
- Show your work, as partial credit will be given.
Write neatly and to the point.
State algorithms at an abstract level. If appropriate, you may use
algorithms from the lectures and the text as subroutines.
Questions
- Define the class NP, a polynomial transformation, and the class NP-Complete.
Consider a known NP-complete problem
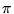 .
What is currently known about the best algorithm for
.
What is currently known about the best algorithm for 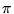 ? What would
be the implication of finding a deterministic polynomial time algorithm
for
? What would
be the implication of finding a deterministic polynomial time algorithm
for 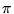 ?
?
- Prove that if the weights are distinct, then there is a unique
minimum spanning tree.
- Work out Krushkal's Smallest-Edge-First algorithm on the following
weighted undirected graph to find a minimum spanning tree (MST)
starting at node
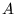 . Show the partial forest and the status of
the working data structures (employing C-Find and W-Union)
as you choose edges. Union two trees
of same weight such that root of the first tree becomes the overall root.
. Show the partial forest and the status of
the working data structures (employing C-Find and W-Union)
as you choose edges. Union two trees
of same weight such that root of the first tree becomes the overall root.
- Workout MST based heuristics for TSP problem on the following completely
connected weighted graph.
- Anser true/false and give one-sentence justification.
- With current knowledge, an NP-complete problem will require
exponential time even on a parallel computer with polynomial
number of processors.
- To determine whether a graph is bipartite is NP-Complete.
- A dynamic programming solution is bottom up, where as its
memoized version is top-down.
- Using Cooks theorem, to show that Hamiltonian Cycle problem is
NP-complete, one must show a polynomial reduction of Satisfiability
to Hamiltonian Cycle.
- Kruskal's minimum spanning tree algorithm can be categorized as
a dynamic programming algorithm because of the optimality of the
substructures and the fact that one builds larger solution from
smaller ones.
- If a problem can be shown to be in class NP,
it means that the problem cannot be in class P.
- An independent set in a graph is a set of nodes with no edges
among those nodes. Therefore, if a graph is properly colored
using 8 colors, then it has 8 independent sets.
- If one finds a polynomial algorithm for Satisfiability problem,
then all known problems will be in class P.
- Prove that
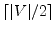 iterations of Bellman Ford all-to-all shortest
path algorithm are sufficient with
the following changes.
The nodes of a graph
iterations of Bellman Ford all-to-all shortest
path algorithm are sufficient with
the following changes.
The nodes of a graph  are indexed from 1 through
are indexed from 1 through 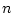 ,
thus partitioning
,
thus partitioning  into
into 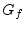 and
and 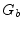 such that
such that 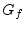 (respectively,
(respectively, 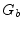 ) contains only those edges
which have their source node indexed lower (higher) than their destination
node. Each iteration of Bellman Ford algorithm is carried out in two
phases: Phase 1 (respectively, Phase 2) relaxes the edges of
) contains only those edges
which have their source node indexed lower (higher) than their destination
node. Each iteration of Bellman Ford algorithm is carried out in two
phases: Phase 1 (respectively, Phase 2) relaxes the edges of 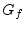 (
(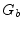 )
in the order of increasing (decreasing) source index.
Hint: How are the edges in a shortest path arranged with respect to
the two graphs
)
in the order of increasing (decreasing) source index.
Hint: How are the edges in a shortest path arranged with respect to
the two graphs 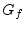 and
and 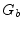 ?
?
- Given a graph
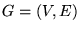 , and independent set is a subset of nodes
, and independent set is a subset of nodes
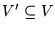 such that no two nodes in
such that no two nodes in 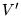 has an edge between them.
(i) State the decision problem associated with independent set problem (use standard
format: Instance followed by Question), and (ii) show that it is in class NP
(give Guess, Checking algorithm, and Analysis showing that time to
guess and check is bounded by a polynomial in length of the instance).
has an edge between them.
(i) State the decision problem associated with independent set problem (use standard
format: Instance followed by Question), and (ii) show that it is in class NP
(give Guess, Checking algorithm, and Analysis showing that time to
guess and check is bounded by a polynomial in length of the instance).
- Show that clique problem can be polynomially
reduced to the independent set problem (IS) as defined in the previous question.
That is, (i) show a transformation of a generic instance of Clique to
an instance of IS, and prove that (ii) the transformation is answer-preserving
and that (iii) it can be carried out in polynomial time.
For (i), simply state the transformation in 1-2 sentences.
For (ii), use 2-3 sentences to argue why a k-size clique in the original
graph must mean k'-size independent set in the transformed graph, and vice versa.
Here,
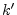 is assumed to be the integer
parameter in the instance of IS obtained from
that of Clique's, and your transformation in (i) will specify the relationship
between
is assumed to be the integer
parameter in the instance of IS obtained from
that of Clique's, and your transformation in (i) will specify the relationship
between 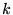 and
and 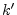 .
For (iii), simply give the time complexity of your transformation and
the order of the length of the Clique's instance. Then, argue that
the former is bounded by a polynomial in the length of the Clique's instance.
.
For (iii), simply give the time complexity of your transformation and
the order of the length of the Clique's instance. Then, argue that
the former is bounded by a polynomial in the length of the Clique's instance.



Next: Student Information
Up: root
Previous: Sample Test 2
Sushil_Prasad
2014-08-26
 are indexed from 1 through
are indexed from 1 through  into
into