


Next: Similarity to Matrix Multiplication
Up: No Title
Previous: No Title
1. Bellman-Ford (adj. list representation) n times 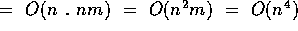 for dense graphs
for dense graphs
2. Dijkstra's 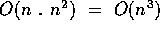 for dense graphs
for dense graphs
(priority queues of edges) 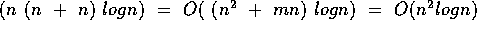 for sparse graphs
for sparse graphs
- We will do 2 dynamic programming algorithms with tight nodes (small coefficients) on
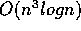 and another
and another
with 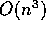
- Goal: Create n x n matrix of shortest-path distances
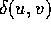
- Graph Representation (adj. matrix)
-
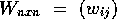 of edge weights.
of edge weights.
-
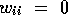
- Let
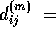 weight of shortest path from i to j that uses at most m edges
weight of shortest path from i to j that uses at most m edges
-
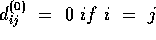 , else
, else 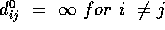
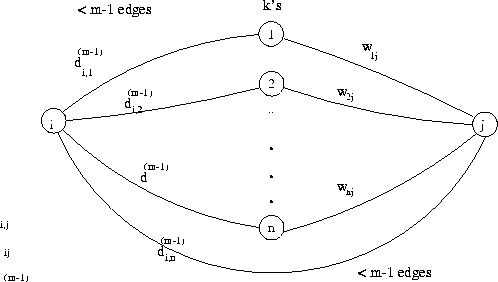
-
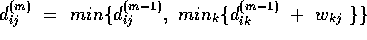
-
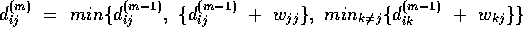
-
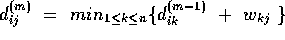
- Answer:
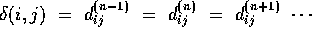
- Pseudo-code for "Relaxation Step"
- for
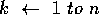
- if
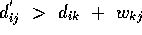 then
then 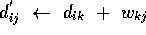
- Time
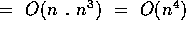
Shekib Yonis
Tue Nov 17 14:10:00 EST 1998
![]() for dense graphs
for dense graphs![]() for dense graphs
for dense graphs![]() for sparse graphs
for sparse graphs