while (TRUE) do
Repeat Decrement j until ![]()
Repeat Increment i until ![]()
if ![]()
then exchange ![]() and
and ![]()
else return ![]()
endwhile
;
;

while (TRUE) doRepeat Decrement j until
![$A[j] \leq x$](img104.gif)
Repeat Increment i until![$A[i] \geq x$](img105.gif)
if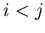
then exchangeand
![$A[j]$](img108.gif)
else return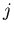
endwhile
Why do ![]() and
and ![]() never get out of array bounds?
never get out of array bounds?
![]() comparisons
comparisons
![]()
![]()
Balance Partitioning: