


Next: Applying Pumping Lemma
Up: Properties of Regular Sets
Previous: Properties of Regular Sets
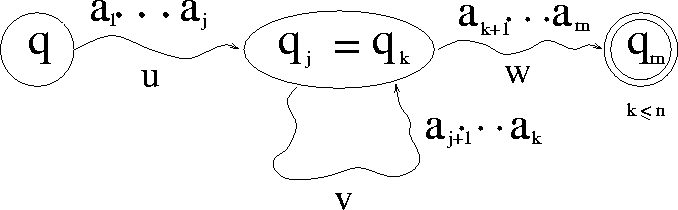
Figure 1: Paths from 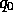 to
to 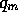 .
.
Suppose n states in an FA.
If 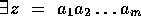 , with
, with 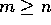
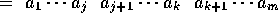
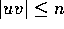
If 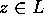 then
then 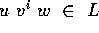 for
for 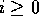 .
.
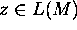
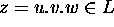
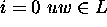
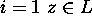
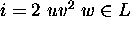
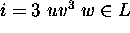
- Pumping Lemma: Let L be a regular set. Then there is a constant
n such that if z is any word in L, and
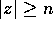 ,
then we may write
,
then we may write  in such a way that
in such a way that 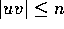 ,
, 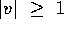 ,
and for all
,
and for all 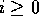 ,
, 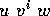 is in L.
is in L.
Furthermore, n is no greater
than the number of states of the smallest FA accepting L.
Sushil Prasad
Tue Mar 21 14:10:23 EST 2000
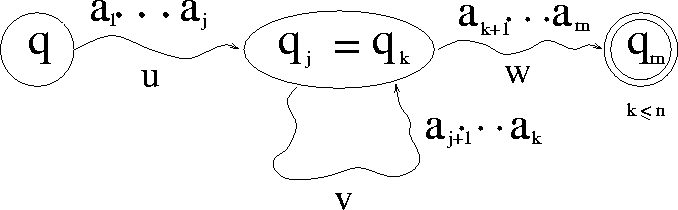
![]() , with
, with ![]()
![]()
![]()
![]() then
then ![]() for
for ![]() .
.![]()
![]()
![]()
![]()
![]()
![]()