d(s) = 0
- for each edge
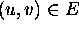
- if d[v]>d[u]+w(u,v)
- then
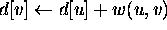
- then
- if d[v]>d[u]+w(u,v)
- if d[v]>d[u]+w(u,v)
- then no solution
- then no solution
Lemma: ![]() always.
always.
First part of Lemma 25.5, section 25.1
Lemma: Bellman-Ford Algorithm is correct.