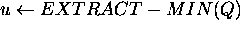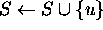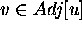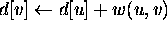DIJKSTRA's ALGORITHM

Let all weights be non-negative. Uses a priority queue Q. DIJIKSTRA(G)

for each ,

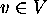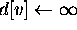
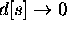
Shortest Path Tree

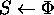
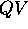prioritized by their d[] labels.

while

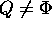
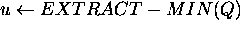
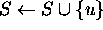
for each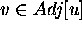

if d[v] > d[u]+w(u,v)
then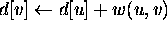

Correctness: Prove that whenever u is added to S,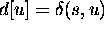
Theorem 25.10
Proof: Basically same as in book, but derives a different contradiction.
Figure 25.6
Note that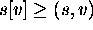
(because lemma proved for Bellman-Ford above was just about relaxation, didn't depend on order of relaxing edges)
Let u be first vertex picked such that shorter path than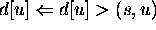
Let y be first vertex 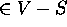on actual shortest path from s to u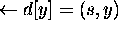

Because:

d[x] is set correctly for y's [predecessor 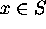on the shortest path (by choice of u as first choice for which that's not true)

when put x into S, relaxed (x,y), giving d[y] correct value,
d[u]> (s,u)
= (s,y)+ (y,u) (optimal substructure)
=d[y]+ (y,u)
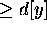(no negative weights)

But 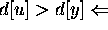algorithm would have chosen y to process next, not u.
Contradiction.