


Next: LOWER BOUND
Up: SORTING BY SPLITING
Previous: Quicksort: Partitioning II
Assume
- all keys distinct
- all permutations equally likely
Probability that split point is 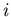 ,
for
,
for
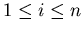 , is
, is 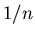
Let
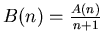 (Changing Variable)
(Changing Variable)
Since 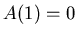 ,
, 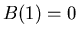
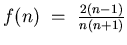 continuous decreasing function
continuous decreasing function
Sushil_Prasad
2014-09-25
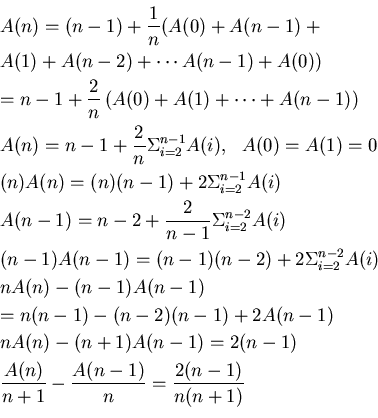
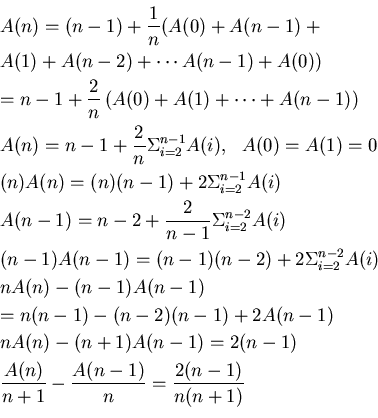
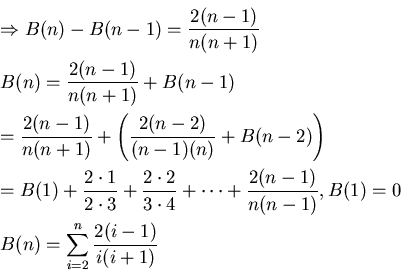
![\begin{eqnarray*}
&&B(n)\leq \int_{2}^{n} f(x)dx, f(1)=0\\
&&\frac{2(x-...
...(n+1)\log n\ [0.5cm]
&&\Rightarrow A(n)\leq 1.4(n+1)\log_{2} n
\end{eqnarray*}](img7.png)