- each accomplishes in undoing one environment
5 1 4 7 2 has inversions (5,1),(5,4),(5,2),(4,2),(7,2)
(n n-1 ...2 1) has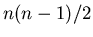 inversions
inversions
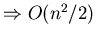 lower bound
lower bound
example: a b c - there are 3! outputs.
(for n numbers there are n! outputs)
Every decision tree to sort n numbers must have atleast n! leaf nodes
Every decision tree to sort n numbers must have atleast 2n! - 1 nodes
Every decision tree to sort n numbers must have depth atleast
Depth is the lower bound worst case time complexity for this class of algorithms