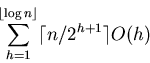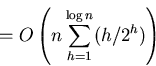Heapsort Construction

Construct Heap:

for 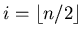$i= \lfloor n/2 \rfloor$ downto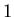 $1$

Restore-heap($i$)

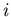Time Complexity of Iterative Algorithm for Heap Construction:

$$\sum_{h=1}^{\lfloor\log n\rfloor}\lceil n/2^{h+1} \rceil O(h)$$

$$=O\left (n\sum_{h=1}^{\log n} (h/2^{h} )\right)$$

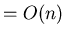$=O(n)$ (pp. 135)


Consider $\sum_{h=1}^{\log n}h/2^{h}$
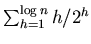
Let

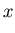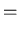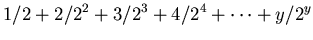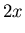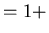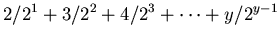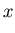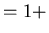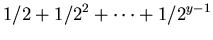$$x = 1/2+2/2^{2}+3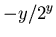/2^{3}+4/2^{4}+ \cdots+y/2^{y}$$ (1)

$$2x =1+ 2/2^{1}+3/2^{2}+4/2^{3}+\cdots+y/2^{y-1}$$ (2)

$$x =1+ 1/2+1/2^{2}+\cdots+1/2^{y-1}$$ (3)

$$-y/2^{y}$$ (4)

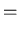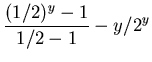$$= \frac{(1/2)^{y}-1}{1/2-1}-y/2^{y}$$ (5)

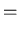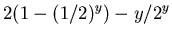$$= 2(1-(1/2)^y)-y/2^{y}$$ (6)

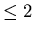$$\leq 2$$ (7)