


Next: Priority Queue employing Heap
Up: Heap Sort
Previous: Heapsort Construction
Construct-Heap(n):
- construct left subheap
- construct right subheap
- Restore-heap(
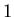 )
)
Time Complexity:
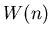 |
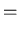 |
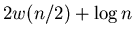 |
(8) |
| |
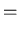 |
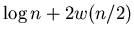 |
(9) |
| |
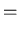 |
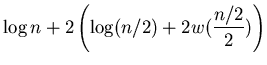 |
(10) |
| |
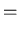 |
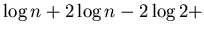 |
(11) |
| |
|
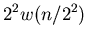 |
(12) |
| |
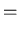 |
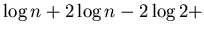 |
(13) |
| |
|
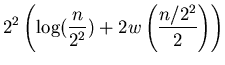 |
(14) |
| |
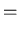 |
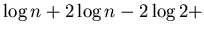 |
(15) |
| |
|
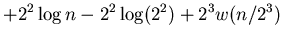 |
(16) |
| |
|
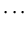 |
(17) |
| |
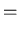 |
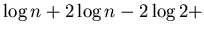 |
(18) |
| |
|
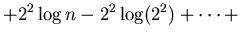 |
(19) |
| |
|
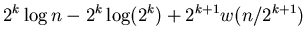 |
(20) |
| |
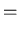 |
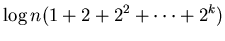 |
(21) |
| |
|
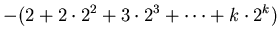 |
(22) |
Here, we assume that 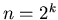 so
so 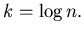
Let
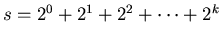
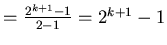
To derive this formula, one can follow these steps:
Thus,
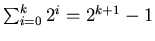
Likewise, let
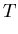 |
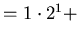 |
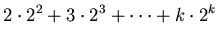 |
(26) |
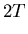 |
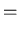 |
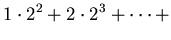 |
(27) |
| |
|
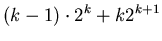 |
(28) |
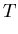 |
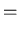 |
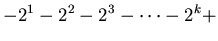 |
(29) |
| |
|
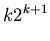 |
(30) |
| |
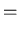 |
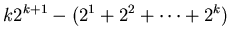 |
(31) |
| |
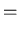 |
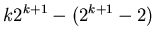 |
(32) |
| |
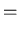 |
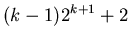 |
(33) |
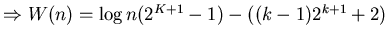
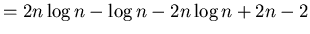
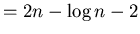
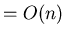



Next: Priority Queue employing Heap
Up: Heap Sort
Previous: Heapsort Construction
Sushil_Prasad
2014-09-25
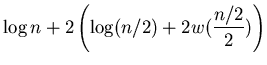
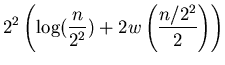
![]() so
so ![]()
![]()
![]()