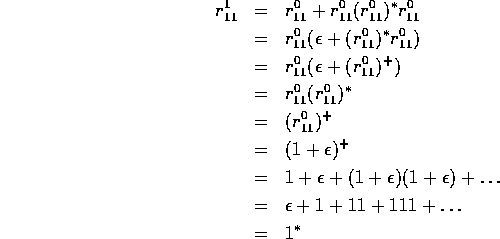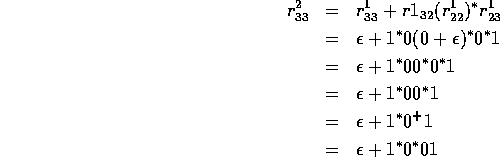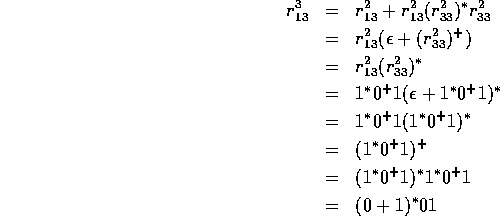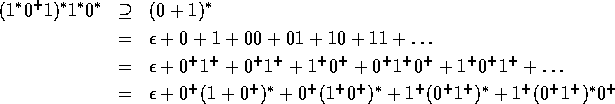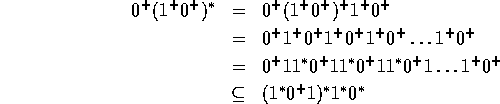Proof: Let L be accepted by a DFA
Let 
= Set of strings that take M from 
to 
such that all
intermediate states have numbers 
.
= Set of string x such that 
and 
for y a prefix of x, 
or x,
then 
.
Recursively,
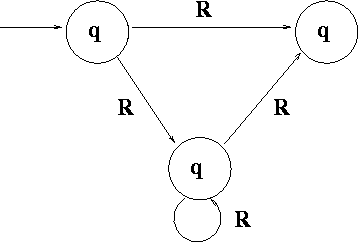
Figure 14: Possible Paths for .
We show that for each i,j,k, is denoted by a RE 
,
for 
.
Induction on k:
Basis: k=0
denoted by 
if empty; 
if i=j.
Else, if 
, then 
for each
such symbol that takes to .
If i=j, then 
.
Hypothesis: For each l,m, there exists an RE 
such that 
.
Induction:
